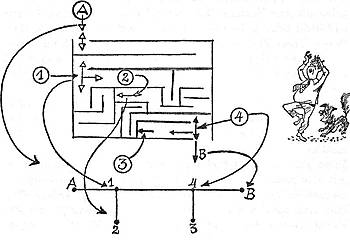
Wir tragen solche Punkte mit kleinen Pfeilchen ein und versehen jeden mit einer Nummer. Dann verbinden wir alle Punkte, die auch im Objekt miteinander verbunden sind, durch eine Linie oder einen Bogen. Unser Bild enthält jetzt nur noch die wesentlichen Eigenschaften des Labyrinths. Wir entnehmen daraus, dass man von A nach B kommen kann und dass man dazu über 1 und 4 gehen muss.
Diese Abbildung kann man nicht umkehren. Man kann aus dem Bild das Labyrinth nicht rekonstruieren, nicht einmal angenähert, und sicherlich lassen sich viele Labyrinthe in ein und dasselbe Bild abbilden.
Unser hier gefundenes Bild nennt man auch einen Graphen, und es gibt eine ganze Graphentheorie zur theoretischen Behandlung derartiger Gebilde. Sie ist ein wichtiges Werkzeug für den Kybernetiker. Eine derartige Abbildung nennt man in der Kybernetik auch eine Transformation, das erzeugte Bild nennt man Modell. Mit diesen Begriffen wird klar, warum man bei der Modellbildung keine identische Abbildung anstrebt. Vielmehr will man das Modell gerade von unerwünschten Komplikationen freihalten. Man legt in die Abbildungsfunktion (deren Eigenschaften übrigens in der mathematischen Disziplin der Topologie studiert werden) den Blickwinkel hinein, den man für eine bestimmte Untersuchung braucht. Boss Ashby hat dies in einem Aufsatz "Simulation of a Brain" (Simulation eines Gehirns) so formuliert: "Wenn etwa ein Arzt aus Gelatine ein Modell macht, das genau so gestaltet ist wie ein Gehirn, um zu studieren, wie Stoßwellen hindurchwandern, und wenn andererseits ein Elektroingenieur ein Netz von Drähten und elektrischen Bauteilen als sein Gehirnmodell aufbaut, um festzustellen, wie elektrische Impulse durch das Gehirn wandern, so ist jedes der beiden Modelle sinnvoll. Trotzdem haben Sie keine gemeinsame Stelle, von der aus man sie vergleichen könnte."
Diese Einsicht ist für die Kybernetik sehr wichtig.
Die Disziplinen Topologie und Graphentheorie sind für die Kybernetik fundamental, wenngleich dies zunächst nur von sehr stark methodisch orientierten Kybernetikern erkannt und appliziert wird.
Begriff des Modells
Die kybernetische Wissenschaft hat den Begriff des Modells sehr präzisiert, und zwar dadurch, dass sie den Zusammenhang zwischen Modellen (die ja in einer gewissen Weise stets Abbildung einer Wirklichkeit oder eines wirklichen Sachverhaltes sind) und der mathematischen Abbildung (etwa der topologischen) ausgenutzt hat. Dabei ist von vornherein klar, dass es sich tatsächlich um eine Ab-Bildung handelt, also nur um ein Bild des abgebildeten Sachverhaltes.
Die einfachste und damit auch uninteressanteste Abbildung einer Gegebenheit in ein Bild (die Abbildung eines Objektraumes in einen Bildraum, wie sich die Mathematiker ausdrucken) ist die Identität, bei der Bild und Objekt vollständig übereinstimmen. Alle andern Abbildungen haben diese Art der Übereinstimmung nicht mehr. Vielmehr konstruiert man sie gerade so, dass nur diejenigen Eigenschaften auf das Bild übergehen, die wesentlich sind. Die Mathematiker charakterisieren Eigenschaften etwa von geometrischen Gebilden gerade dadurch, wie sie sich bei bestimmten Abbildungen verhalten.
Dabei muss man sich von der Vorstellung trennen, dass eine Abbildung nur dann zustande käme, wenn man den formalen Zusammenhang kennt, der zwischen Objekt und Bild und zwischen Bild und Objekt (das sind gegebenenfalls zwei verschiedene Dinge) besteht. Ein kurzes Beispiel mag dies erläutern. Unsere Zeichnung zeigt ein einfaches Labyrinth, wie man es gelegentlich in Sonntagszeitungen findet. Auf den ersten Blick ist es gar nicht so einfach, den Weg von A nach B zu finden oder festzustellen, ob man überhaupt von A nach B gelangen kann. Deshalb streben wir eine Abbildung des Labyrinthes in ein Bild an, das uns den Durchblick erleichtert. Zwei Dinge sind interessant. An welchen Stellen kann man einen Weg verzweigen? Und wo endet ein Gang - sei er tot, sei es ein Ein- oder Ausgang?